מה *לא* לימדו אותנו באוניברסיטה על מבני-נתונים? חלק ב'

בפוסט הקודם, הצגתי שני עקרונות חשובים של מבני-נתונים שלא הבנתי עד שלב מאוחר יותר בקריירה: חוק המספרים הקטנים (אמרו לי, אבל לא הדגישו עד כמה) ועיקרון המקומיות של נתונים.

בפוסט הזה אני רוצה לגעת בעוד כמה עניינים מעוררי-מחשבה:

• מדוע HashTable לא באמת פועל ב (Θ(1?
• מדוע עבודה על איברים בודדים במערך ממוין - מהירה יותר מעבודה על מערך לא ממוין? 
• כיצד Regular Expressions עלולים להוסיף סיבוכיות מיותרת?
• מהו אלגוריתם המיון היעיל והנפוץ ביותר - שאתם כנראה לא מכירים?

בואו נתחיל!

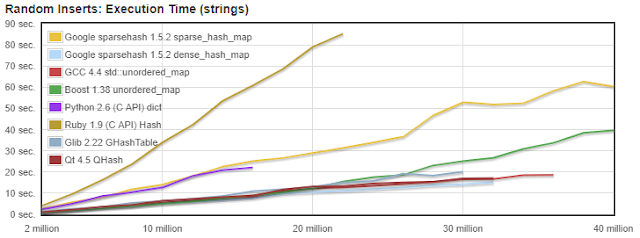לא כל ה hashtables נולדו שווים. זמני הכנסה של מיליוני איברים.

מיתוס: HashTable מכניס ושולף איברים ב (Θ(1

בקורס מבני-נתונים כנראה ולימדו אותנו ש HashTable מכניס/מוחק/שולף איברים בזמן קבוע - ולכן ניתן להסיק שזה זמן טוב מאוד.

זה לא מדויק. זהו פישוט משמעותי - שאכן שימושי לעבודה בסטים קטנים של נתונים.
רוב הזמן אנו עובדים עם HashTables המחזיקים מאות או אלפי איברים לכל היותר. חוק המספרים הקטנים חל כאן - ואין טעם לנסות ולחפש אופטימיזציה.

אבל, כאשר אנו מטפלים בכמויות גדולות של נתונים, חשוב להבין:

זמן הריצה של ה hash function איננו אפסי. פונקציית hash אורכות זמן, בד"כ כפונקציה יחסית לקלט.
אם נניח, לצורך הפשטות, שהמפתח (key) ב HashTable הוא מחרוזת, אזי יהיה נכון לומר שזמן הכנסה של איבר הוא (Θ(k כאשר הוא k תלוי באופן ישיר באורך המחרוזת. זמן הביצוע תלוי גם בפונקציית ה hash הספציפית שנבחרה, ופונקציות hash "איכותיות" המספקות פיזור קרוב יותר לאחיד - רצות לאורך זמן רב יותר.

במקרה והמפתח של ה HashTable הוא אובייקט מורכב - ייתכן וזמן הריצה יהיה משמעותי.

חשוב לזכור שאת פונקציית ה hash לא מחשבים רק בהכנסה של איבר, אלא גם בכל שליפה.
כאשר יש התנגשויות (collisions) אזי יש לקחת בחשבון גם n קטן של השוואות.

נניח ועלינו לשלוף מתוך סט של M איברים - כ m איברים. עומדות לפנינו 2 ברירות:

• לשלוף m איברים מתוך HashTable, בזה אחר זה.
• לסרוק את כל המערך בגודל M ולמצוא את האיברים.
• להזכיר: ה HashTable משתמש במערך, מאחורי הקלעים.

בהסתכלות נאיבית נראה שהבחירה היא בין (Θ(M לבין (Θ(m (כאשר M > m) - בחירה קלה למדי.

בפועל הבחירה היא בין (Θ(M לבין (Θ(m*k, כאשר סביר להניח ש k (זמן הריצה של ה hash function כתלות באורך הקלט) יהיה גדול בעשרת מונים, לכל הפחות, מפעולת שליפה של איבר בודד ממערך.
בסריקה סדרתית של המערך, כפי שאנו יודעים - אנו נהנים גם Data locality של הנתונים. בלוקי-הזיכרון יובאו לזיכרון פעם אחת, וינוצלו במלואם.


אפשר לומר שאם M/m < 10 - אזי בוודאי עדיף לסרוק את המערך.
הדבר עשוי להיות נכון גם ל M/m < 100 ואולי אף יותר - יש לבדוק כל מקרה לגופו.


מכאן, כדאי לזכור:

• כאשר יש לנו בעיות ביצועים, במיוחד בלולאה ששולפת ומכניסה ל HashTable - אל תניחו שזמן השליפה מתוך ה HashTable הוא זניח.
• שימוש באובייקט עסקי (למשל: Customer) בתור מפתח ל HashTable עשוי להיות מיפוי עסקי מבריק.
• כאשר חוק המספרים הקטנים פועל - אין בעיה.
• כאשר אנו נדרשים לספק ביצועים גבוהים על כמויות גדולות של נתונים - אובייקט גדול כמפתח עשוי להיות רעה חולה.
• שווה גם להזכיר את העניין הידוע בג'אווה שאם אתם דורסים את מתודת ()equals עליכם לדרוס גם את ()hashCode, וליהפך.

Benchmark פשוט שהרצתי כמה פעמים בכדי להראות שהכנסה ל HashTable היא לא כמו הכנסה ל ArrayList. להמחשה בלבד.

חזרה ל Data Locality

נושא מרכזי שעסקתי בו בפוסט הקודם היה Data Locality: איזו יתרון יש, בארכיטקטורת מחשבים בת-זמננו, לגישה לזיכרון רציף כך שהנתונים יוגשו מה Caches הקרובים ביותר (L1>L2>L3). אנו רוצים לצמצם ככל האפשר גישות לזיכרון הראשי או (חס וחלילה!) לדיסק.

כ 85% משטח ה CPU המודרני מוקצה ל Caches, וכמעט כל השטח קשור באופן ישיר לאכסון או העברה יעילה של נתונים. Data Locality איננו פרט שולי - אלא עקרון מרכזי בארכיטקטורה של מעבדים מודרנים.

הנה הרצאה של Herb Sutter (מחבר סדרת הספרים ++Exceptional C) בנושא.
עוד מקור מוצלח הוא המצגת Pitfalls of OO Programming - המיועדת במקור למפתחי מנועי משחקי-מחשב, היכן שהשיקולים הללו הם מלאכה יום-יומית.

החשיבה על Data Locality איננה נכונה רק למבני-נתונים, אלא לכל רצף ארוך של פעולות שאנו מבצעים. פעולות כאלו לרוב יכללו מבני-נתונים - אך לא תמיד.

עקרון ה Locality מגיע בשני אופנים:

1. מקומיות זמנית - כאשר ניגשים ל(בלוק) זיכרון, סביר מאוד שניגש שוב לאותו בלוק בזמן הקרוב. באופן אידאלי - אותו בלוק זיכרון עדיין יהיה ב cache קרוב, ולא נצטרך להביא אותו שוב.
2. מקומיות מרחבית - אנו שומרים נתונים הקשורים זה-לזה בקרבה פיסית בזיכרון, כך שגישה לבלוק אחד מצדיקה הבאה של בלוקים "שכנים" מתוך ידיעה שיש סבירות גבוהה שיהיו גישות בזמן הקרוב גם לנתונים הללו.

למשל: כשעוברים על מערך דו-מימדי עדיף הרבה יותר לעבור שורה-שורה (כלומר: על איברים במערך הפנימי ברצף) מאשר לעבור על הטורים ו"לקפוץ" כל פעם בין המערכים הרציפים שהוקצו.

יעילות ה cache בשני מימושים דומים. סדר הגישה העדיף כמובן תלוי במימוש הספציפי של שפת התכנות / סביבת הריצה שאנו עובדים בה.

דוגמה עדכנית נוספת יכולה להיות Streams:

• כל הפעולות ב Stream יפעלו ברצף איבר-איבר. הדבר מאפשר מקומיות זמנית ברמה הגבוהה ביותר של caching, ב registers של המעבד (ה cache המהיר ביותר) - מה ברוב הפעמים יתרום לביצועים.
• כאשר יש ברצף הפעולות פעולות "רוחביות" (כגון sorting) אזי דווקא עדיף להשתמש ב collection ולא ב stream - בכדי ליהנות ממקומיות מרחבית.

בשפת קוטלין ברירת המחדש היא עבודה ב collections, ועל מנת לבחור ב stream יש להשתמש ב ()asSequence.

כמובן שכל היתרונות הללו בטלים בשישים - כאשר מדובר בחוק המספרים הקטנים. כלומר: אל תחשבו עליהם אפילו - אם מדובר במאות איברים או פחות.
כאשר אנו עובדים על כמות קטנה של נתונים - הם ככל הנראה יתאימו ל cache, גם אם יוגשו מעשרות בלוקים שונים של זיכרון. הדבר כן עשוי לידי ביטוי אם אנו מבצעים את הפעולה הזו שוב ושוב - עבור נתונים שונים.

מדוע עבודה על איברים בודדים במערך ממוין - מהירה יותר מעבודה על מערך לא ממוין? 

כמובן שזה לא המקרה תמיד, אבל זה בהחלט עשוי לקרות.

הביטו שניה בקוד הבא ונסו לחשוב כיצד הדבר קורה:

העניין פה הוא אופטימיזציה ברמת המעבד הנקראת Branch Prediction.

בגדול, ה CPU עובד ב pipeline ארוך של פעולות. כלומר: הפעלת רצף פעולות יעלה רק מעט יותר מהפעלה של פעולה בודדת.
כאשר יש להמתין לתשובה בבחירת הפעולה הבאה - הרצף נשבר, והיתרון בהפעלה של pipeline ״באוטומט״ - אובד.

מתי זה שימושי?
למשל כאשר יש משפטי if בולאנים ולאחריהם פעולה פשוטה. בזמן שממתינים לתוצאה של תנאי ה if - המעבד יכול לבצע כבר פעולה נוספת באותו ה pipeline.

במקרה שלנו יש Branch prediction על הפעולה : (if (data[c] >= 128.
השורה העוקבת היא פעולה פשוטה שהמעבד יכול להפעיל בזמן שהוא ממתין לתוצאת ה if. האלטרנטיבה (תחילת איטרציה חדשה) - היא כבר פעולה כבדה יותר. מכאן סביר שהמעבד יבחר בשורה העוקבת ו״ידחוף״ אותה ל pipeline.

אם הוא צדק בניחוש - הוא ייקח את תוצאת החישוב שאליה הגיע (התוצאה של הפעלת ()data[c].toLong)  - וישתמש בה.
אם טעה - לא נורא. הוא "יזרוק" את מה שהכין - וימשיך ב branch השני (במקרה הזה - קידום הלולאה). בכל מקרה הוא לא היה מסוגל לפעול מהר יותר.

כאשר המערך ממוין, ובמיוחד במקרה כמו שלנו בו יש טווח מאוד מצומצם של 256*2 ערכים אפשריים - הניחושים של ה CPU עומדים להיות טובים מאוד (אפשר לומר: על סף האופטימליים).

לכן, כאשר המערך ממוין, הטרנספורמציה ל long מתרחשת בתוך אותו ה pipeline כמעט תמיד ובעלות זניחה, בעוד כאשר המערך לא ממוין, זה יקרה רק לפעמים (כ 50% מהמקרים).
כפי שניתן לראות - הפערים בזמני הביצוע הם משמעותיים למדי (ב ++C הפערים מגיעים לכמעט פי 10).


המסקנה היא לא לתכנן את הקוד שלכם בכדי שינצל נכון branch prediction. אם זה מה שהבנם - אז הבנתם לא נכון.
הבאתי את הדוגמה מכיוון שהיא מעניינת ועשויה לעורר את החשיבה.
לכו עם המעבד - ולא נגדו. זה ישתלם לכם. ברמה היום-יומית התרגום של זה הוא לנסות להקפיד על Data Locality - בעבודה על סטים גדולים של נתונים.

מילה על Regular Expression

Regex אינם מבני-נתונים. מה הם עושים כאן בפוסט?!

הכללתי את הנושא, כי הוא כולל אלמנטים משיקים.
פגשתי לא פעם אנשי-תוכנה שהיו משוכנעים שאם הם יגדירו ביטוי כ Regex ו״יעברו שלב קומפילציה" (בניית ה matcher) - אזי מובטח להם שה Regex יהיה יעיל יותר מקוד שיכתבו.

Regex הוא בגדול כלי productivity: לכתוב ביטוי Regex ייקח, ברוב הפעמים, פחות זמן מלכתוב קוד מקביל שיבצע פעולה דומה.
זמני הריצה של ה RegEx תלויים מאוד בביטוי, כאשר ביטויים מסוימים מחושבים ב (O(1, אחרים ב (O(n, אולי (O(n^2 ועד סיבוכיות שלא ניתן לתאר. הם בהחלט לא חייבים להיות (O(n.

למשל, לפני זמן לא רב נתקלתי ב Unit Test שזמן הריצה שלו עלה מ ms בודדים - לשלוש דקות בגלל הרצה של Regex מסובך למדי.
הנה סיפור על Regex שרץ לאורך 5 יממות - והוחלף ע"י כלי אחר שעשה את העבודה ב 15 דקות (פשוט ירידה בסיבוכיות - אין כאן קסמים).

בקיצור:

• אל תניחו שזמן הריצה של Regex הוא לינאי או קרוב לכך. הכל תלוי בביטוי הספציפי.
• כש Regex הופך לבעיה, בדקו כיצד ניתן לשפר את הביטוי בכדי לקבל סיבוכיות מסדר גודל קטן יותר.
• תמיד יש את האופציה הלגיטימית לכתוב custom code - ברמת סיבוכיות ואופטימיזציה גבוהה יותר.

בקצרה: מבני-נתונים ואלגוריתמים מקובלים - שכדאי להיות מודעים אליהם

מיון

שתי שפות התכנות הנפוצות ביותר בעולם כיום הן, ככל הנראה: ג'אווה ופייטון [א].

מה אלגוריתם החיפוש של הספריה הסטנדרטית שלהן?

• QuickSort (היה נכון פעם ל ++C) - לא.    עדכון: פרמיטיביים בג'אווה ממוינים בעזרת DualPivotQuicksort. יש לו עניין של instability - אך זה לא רלוונטי לפרמיטביים.
• MergeSort (פעם היה בג'אווה) - לא.
• BubbleSort? - אל תהיו מצחיקים!

אז מה? איזה אלגוריתם חיפוש הוא, אחד הרצים בעולם ואחד המוכרים פחות?

TimSort!

אל תתביישו אם לא שמעתם עליו - אבל כדאי להכיר.

בתיאוריה, קיימת הוכחה מתמטית לפיה כל אלגוריתם מיון שאין לו ידע על התפלגות הקלט (למשל: רק מספרים בטווח מסוים) לא יוכל להיות יעיל יותר מ (Θ(n*lgn. 

לא קל להגיע לזמן ביצוע של (Θ(n*lgn - ובד"כ זה בא במחירים אחרים. למשל: זיכרון (כמו MergeSort).

TimSort מצליח "לנצח" את התאוריה במקרים מסוימים (Best Case), ובממוצע להציג שיפור לא רע, בזכות הנחה מעניינת אך בסיסית על הפלגות הנתונים: שהיא לא אקראית לחלוטין. ככל שהיא תהיה פחות אקראית - כך הביצועים שלו יהיו טובים יותר.

TimSort (שקרוי על שם מי שפיתח אותו, טים פיטר, ממפתחי פייטון - זה לא אלגוריתם שהגיע מהאקדמיה) בבסיסו מריץ MergeSort (אלגוריתם שלרוב מבצע טוב מהרגיל) בעוד הוא משתמש ב batches קטנים ב Insertion Sort (גרסה משופרת של ה BubbleSort) - היעיל במיוחד למיון קבוצות קטנות של נתונים.

בנתונים מהעולם האמיתי המידע לא מפוזר באופן אקראי לחלוטין. בעצם: קשה מאוד לייצר נתונים אקראיים לחלוטין. בנתונים ״רגילים״ של מערכים יש בו רצפים, גדולים או קטנים, של איברים ממוינים.

TimSort פועל בגדול באופן הבא:

1. סריקה של הנתונים ואיתור רצפים עולים ורצפים יורדים. אם הרצף יורד - הוא פשוט יהפוך אותו. 
1. הנתונים כבר ממוינים? סיימנו ב (O(n. לא נשמע חוכמה, אבל QuickSort ו MergeSort יבזבזו כאן (O(n*lgn, זה יכול להתתרגם לפי 10 או פי 100 - יותר זמן ריצה.
2. קבוצות של עד 64 איברים - ממיינים בעזרת Insertion Sort, היעיל לקבוצות קטנות של נתונים וגם נהנה מ Data Locality.
3. שימוש ב Merge Sort על מנת למיין את הקבוצות הממוינות - כאשר נשמר איזון בין הקבוצות בעקבות המיון המוקדם.

הנה סרטון המדגים את אופן הפעולה שלו. הנה הסבר מפורט יותר על אופן הפעולה.

שווה להכיר בקיומו: KD-Tree

KD-Tree הוא מבנה נתונים דיי שימושי (אני השתמשתי כמה פעמים) המאפשר לאנדקס נתונים בכמה מימדים.
בעיקרון הוא מקרה כללי של Binary Search Tree (הרץ על מימד אחד), אבל מאפשר לרוץ על כמה מימדים.
אם אנו רוצים לאנדקס 2 מימדים - אז כל שכבה זוגית תבצע חיתוך על ציר x וכל שכבה אי-זוגית על ציר y.
את אותו רעיון אפשר להרחיב ל 3, 4 מימדים ויותר.

במקרה הזה הצומת הראשי מפצל את המרחב על ציר x, ואז הקודוד מתחתיו את ציר y, וחוזר חלילה.

KD-Trees משמשים בבסיסי נתונים, ובכלל, לאינדוקס מרחבים geospatial ("גאוגרפיים"). עצי KD-Tree מסדר 2 מתארים מרחב גאוגרפי (x ו y), בעוד עד מדרגה 3 למשל, עשוי לתאר מרחב + זמן (למשל: היכן הייתה כל מונית בכל רגע נתון).

הרצון לאנדקס מרחב רב-מימדי עשוי להיות רלוונטי למקרים רבים. אינדקס של כמה עמודות בבסיס-הנתונים - מתנהג בצורה דומה. לאינדוקס כשזה יש גם שימושים מדעיים שונים (פיסיקה, ניתוח צבעים כאשר R, G, ו B הם שלושת המימדים, וכו׳).

מבנה נתונים מקביל ל KD-Tree הוא ה R-Tree. בניגוד ל KD-Tree שבו כל node חוצה מרחב, ב R-Tree כל node מתאם מרחב תחום (Rectangle, ומכאן השם) ומכאן למרחבים שלו יכולים להיות חפיפות.



שווה להכיר בקיומו: Skip List

רשימת דילוג (Skip List) היא וריאציה של LinkedList הדומה יותר לעץ מאוזן (כמו עץ אדום-שחור או AVL) - אך המימוש שלה פשוט יותר.

מימוש פשוט לא מעניין אותנו כשיש שיתוף קוד (אחד כותב - רבים משתמשים). כמן כן, למדנו כבר להיזהר ממבני-נתונים עוייני cache כמו רשימות משורשרות ועצים. אז מה הטעם בו?

הייחודיות של ה Skip List היא ביכולת שלו לשרת כמבנה נתונים מוצלח למדי לעבודה מקבילית - תחום שהולך והופך חשוב ושימושי עם ריבוי ה cores בתעשייה.

בבסיס, רשימת דילוג היא כמו רשימה משורשרת. התבוננו רק על הרמה הראשונה (L1) - זו ממש רשימה משורשרת.
מה הבעיה ברשימה משורשרת (מלבד עוינות ל caches)? - שמציאת איבר ברשימה אורכת (O(n וזה יכול להיות יותר מדי.

הפתרון הוא להוסיף רמות דלילות לרשימה - שיאפשרו התקדמות מהירה בעת "סריקת" הרשימה.

הנה תסריט "צמיחת הרמה השנייה": כאשר אנו מוסיפים nodes לרשימה, אנו מבצעים הגרלה של 1:2 כמו הטלת מטבע. אם יצא "עץ" (במקור: "heads") נוסיף node גם ברמה השניה. כך תיווצר לנו רמה שניה דלילה יותר.
באופן דומה אם יש לנו 3 רמות, node שנוסף והוגרל להיות חבר ברמה 2, יוגרל שוב ביחס 1:2 להיות חבר גם ברמה 3.

מספר הרמות ברשימת הדילוג, ייקבע ביחס למספר האיברים שבה. גם ההגרלה (״רמת הדלילות״) לא חייבת להיות 1:2. היא יכולה, למשל, להיות 1:4 - רשימה דלילה יותר.

כאשר אנו מחפשים איבר, למשל בתרשים למעלה את מספר 8, אנו מתחילים מהרמה הגבוהה ביותר, ומבצעים חיפוש דומה מאוד לעץ בינארי. אם ה node הבא גדול מהערך שאני מחפש - נרד רמה ונבקש שם את ה node הבא - עד שמצאנו אותו (או בדוגמה לעיל - 8 לא נמצא ברשימה ולכן לא נמצא).

אם ההסבר לא ברור דיו, אך אתם עדיין מתעניינים - חפשו באינטרנט. זה מבנה נתונים מוכר.


מקביליות

מכיוון שההחלטה כמה רמות להוסיף ל node חדש היא מבוססת על אקראיות (ולא תלויה בשאר המבנה של הרשימה) ל SkipList יש יתרון בהכנסה מקבילית של איברים, שבאמת יכולות להיות פעולה מקבילית ברמה גבוהה (כלומר: לאפשר הרבה מקביליות). במימוש בג'אווה (ConcurrentSkipListMap) משתמשים ב AtomicReference על מנת להגן על הקשר לשאר הרשימה - היכן שיכול להיות race condition. מעבר לכך אין צורך בשימוש ב synchronization או מנעולים (שמגבילים מאוד את כמות המקביליות).

חשוב לציין שהמבנה הזה אינו אידאלי לכל תסריט מקבילי. בג'אווה ה ConcurrentHashMap - מימוש HashTable עם מנעולים על טווחים על המערך שמאחורי-הקלעים, אולי לא יכול לעמוד באותה כמות מקבילית של הכנסות, אך שליפה של איבר היא פעולה מהירה בהרבה (O(k (מול (O(lgn ברשימת הדילוג).
אם למשל, המקביליות היא רק בקריאה - אזי HashMap רגיל יהיה היעיל ביותר.
בקיצור: מקביליות היא עניין מורכב, ולא נכסה אותו כאן...


הערת סיום: לזכותה של המחלקה למדעי המחשב באוניברסיטת בן-גוריון ארצה לציין שכן למדנו בקורס מבני-נתונים על KD-Trees ו SkipLists - וזה היה במקום. תודה רבה, לפרופ' קלרה קדם שלימדה אותנו (מפתיע, אבל אני עדיין זוכר את שמה אחרי הרבה שנים).

סיכום

זהו. על נושא של מבני-נתונים ניתן להוסיף ולהרחיב בלי סוף - אבל מעבר לנקודה מסוימת זה כבר לא תורם ממש (עבור השימושים הנפוצים). כשתתקלו בבעיה מיוחדת - בוודאי תמצאו לה, או תמציאו לה - מבנה נתונים עדיף.

מבני-נתונים הם לא רק תאוריה של סיבוכיות, אלא גם עניין של היגיון בריא והתאמה לצרכים הקצת-יותר ספציפיים שעומדים בפניכם. לא פחות, חשוב לקחת בחשבון את החומרה שמריצה את האלגוריתם ולחתור ל Data Locality. ככל שהשנים עוברות, Data Locality הולך ונהיה פקטור יותר ויותר משמעותי ביעילות של עבודה על קבוצות גדולות של נתונים.


שיהיה בהצלחה!

-----

[א] נכון, גם ג׳אווהסקריפט נפוצה מאוד - אבל קשה לי להתייחס לאלגוריתם המיון המובנה שבה ברצינות.

ראשית הוא ממיין ע״פ סדר לקסיקוגרפי, גם מערך של מספרים:

[7, 44, 3].sort() = [3, 44, 7]

עד ממש לאחרונה, מנוע V8 הסופר-פופולארי לא היה יציב. כלומר: הוא עשוי היה, באופן אקראי, להחליף בין ערכים שהם זהים. זה לא מפריע במספרים - אך עשוי להפריע באובייקטים מורכבים.

דוגמה אחרונה, וחמורה למדי, היא זו:

בעוד מומחים בתחום טוענים בתוקף שהביצה היא זו שקדמה לתרנגולת. למשל: ביצי דינוזאור.